Computing Inversion-Free Mappings by Simplex Assembly
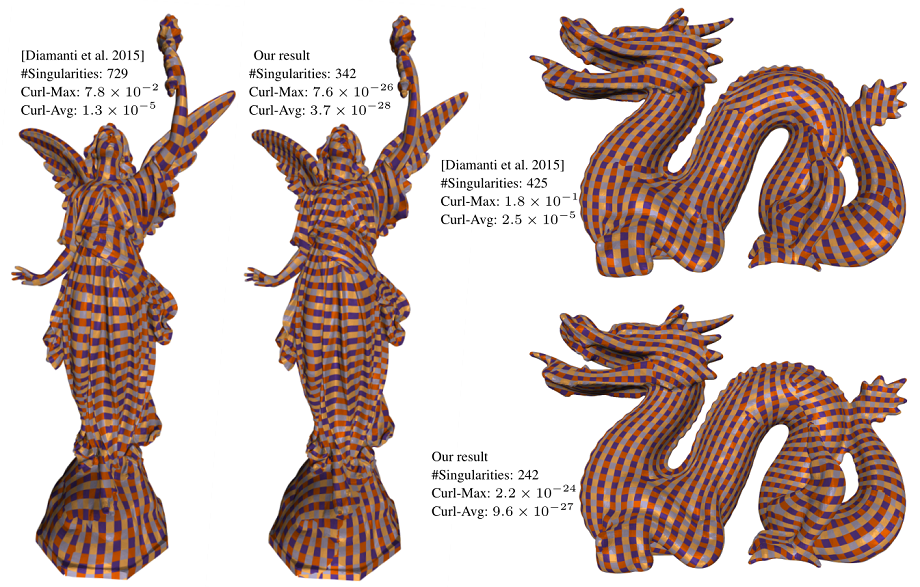
Figure 1:Global seamless parameterization. Compared with [Diamanti et al. 2015], our method maintains the original singularities and has much lower edge-curl values.
Abstract
We present a novel method, called Simplex Assembly, to compute inversion-free mappings with low or bounded distortion on simplicial meshes. Our method involves two steps: simplex disassembly and simplex assembly. Given a simplicial mesh and its initial piecewise affine mapping, we project the affine transformation associated with each simplex into the inversion-free and distortion-bounded space. The projection disassembles the input mesh into disjoint simplices. The disjoint simplices are then assembled to recover the original connectivity by minimizing the mapping distortion and the difference of the disjoint vertices with respect to the piecewise affine transformations, while the piecewise affine mapping is restricted inside the feasible space. Due to the use of affine transformations as variables, our method explicitly guarantees that no inverted simplex occurs, and that the mapping distortion is below the bound during the optimization. Compared with existing methods, our method is robust to an initialization with many inverted elements and positional constraints. We demonstrate the efficiency and robustness of our method through a variety of geometric processing tasks.
Downloads
Paper, Data, Slides, Code (BaiduYun).
Summary
Our goal: Compute inversion-free mappings with low or bounded distortion.
The idea: Our essential idea includes two steps: (1) we first disassemble the simplicial mesh into disjoint simplices that are inversion-free and stay inside the feasible distortion space; (2) we treat piecewise affine transformations as variables and assemble the disjoint simplices by solving an unconstrained optimization problem whose objective penalizes disjoint simplices and restricts the affine mappings inside the feasible distortion space by a simple and novel barrier function that avoid inversion and control distortion.
Applications: Parameterizations, fixed boundary mapping, mesh deformation.
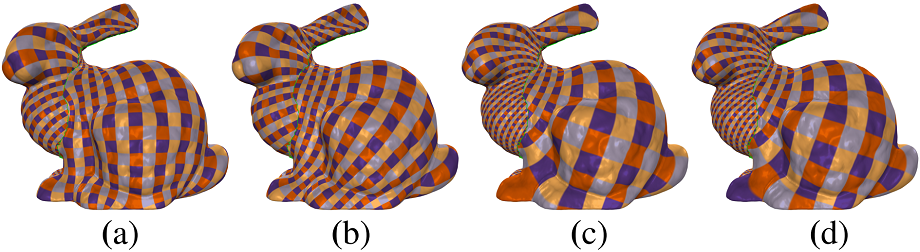
Figure 2: Conformal parameterization for a Bunny model (1251046 vertices). (a) and (b) are the results of [Fu et al. 2015] initialized with a circular convex mapping and the result of Linear ABF [Zayer et al. 2007].(c) FBDM [Kovalsky et al. 2015]. (d) Our result. Our method with the speedup strategy took 10.2 seconds while the AMIPS method [Fu et al. 2015] took 2 hours with the Tutte embedding initialization and 2 minutes with the Linear ABF [Zayer et al. 2007] initialization. FBDM [Kovalsky et al. 2015] took 82.3 seconds to converge using the same bound and the LSCM initialization. The maximal and average conformal distortion of the result of AMIPS (a & b), FBDM (c) and our method (d) are (2.29, 1.006), (2.25, 1.003), (2.50, 1.004) and (2.42, 1.004) respectively. Our method obtains a comparable result in the least time.
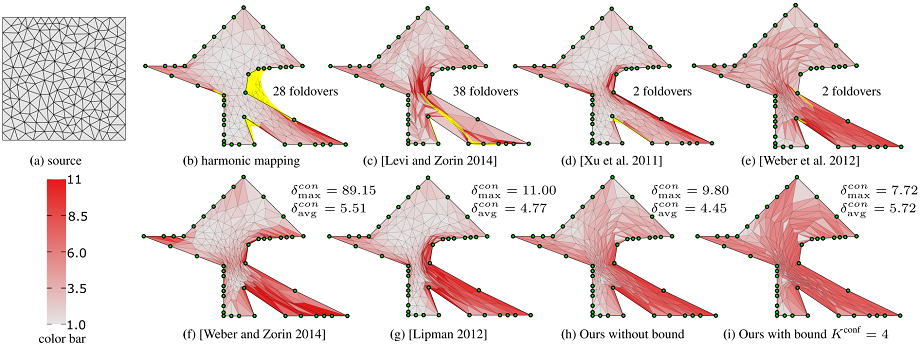
Figure 3: 2D conformal fixed-boundary mapping. A square-shaped triangle mesh (a) is mapped onto a non-convex polygonal domain. A harmonic mapping (b) contains 28 foldovers (colored in yellow). With this poor mapping as initialization, our method can easily achieve inversion-free results with low distortion (\(K^{\textrm{conf}} = \infty\)) (h) and bounded distortion with bound \(K^{\textrm{conf}} = 4\) (i). \(E_m = 0\) in this example. We compare our method with other state-of-the-art methods. The methods of [Levi and Zorin 2014] (c), [Xu et al . 2011] (d) and [Weber et al. 2012] (e) cannot prevent foldovers. The method of [Levi and Zorin 2014] needs to insert 9 additional vertices into the triangulation to guarantee inversion-free results (f). Bounded distortion methods like [Lipman 2012] can find a valid mapping (g), but the bound is hard to determine. It fails when \(\delta^{con}_{bound} < 11\) using the authors' implementation with the defaulting setting. The color on triangles encodes the conformal distortion, with white being optimal.
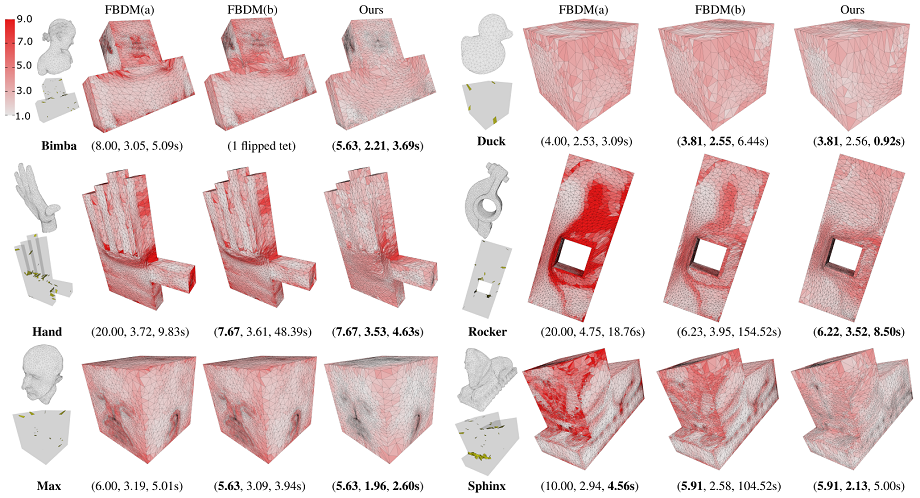
Figure 4: Conformal PolyCube mapping of six models using our algorithm and FBDM with different settings. The initial mappings of FBDM(a) and FBDM(b) are the same as in [Aigerman and Lipman 2013]. The bound of FBDM(a) is the same as in [Kovalsky et al . 2015]. FBDM(b) uses our maximal conformal distortion as the bound. The bottom-left insets show the initial mappings with inverted tetrahedrons (colored in yellow). The boundary tetrahedrons are color-coded using the magnitude of \(\delta^{con}\). The three numbers below each figure report the maximal conformal distortion, average conformal distortion and running time. The number of vertices and tetrahedrons of the models are: Bimba (10790,45422), Duck (2464,12601), Hand (8366,40627), Rocker (12428,60301), Max (9867,40076), Sphinx (10528,43371).
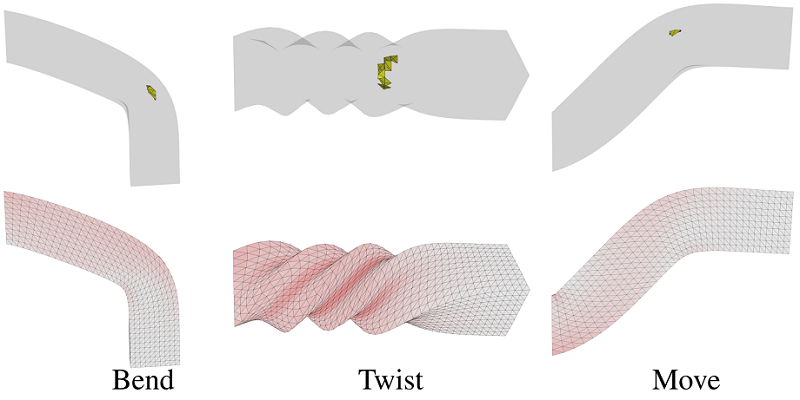
Figure 5: Tetrahedral mesh deformation. Bend, twist and translate a bar. The initial mapping results of the first row are from [Aigerman and Lipman 2013] and contain some inverted tetrahedrons. The second row shows our low distortion and inversion-free results.
Bibtex
@article {Fu-2016-SA,
title = {Computing Inversion-Free Mappings by Simplex Assembly},
author = {Xiao-Ming Fu and Yang Liu},
journal = {ACM Transactions on Graphics (SIGGRAPH Asia)},
volume = {35},
number = {6},
year = {2016},
}