Teaser: Our algorithm generates a small number of developable patches for approximating three models, including a model with three mushrooms, a chair, and a teapot, physically validated using color paper.
Abstract
We propose a novel method to compute high-quality piecewise developable
approximations for triangular meshes. Central to our approach is an evolutionary genetic algorithm
for optimizing the combinatorial and discontinuous fitness function, including the approximation error,
the number of patches, the patch boundary length, and the penalty for small patches and narrow regions
within patches. The genetic algorithm's operations (i.e., initialization, selection, mutation, and crossover)
are explicitly designed to minimize the fitness function.
The main challenge is evaluating the fitness function's approximation error as it requires developable patches,
which are difficult or time-consuming to obtain. Resolving the challenge is based on a critical observation:
the approximation error and the mapping distortion between an input surface and its developable approximation
are positively correlated empirically. To efficiently measure distortion without explicitly generating
developable shapes, we creatively use conformal mapping techniques. Then, we control the mapping distortion
at a relatively low level to achieve high shape similarity in the genetic algorithm.
The feasibility and effectiveness of our method are demonstrated over 240 complex examples. Compared with the
state-of-the-art methods, our results have much smaller approximation errors, fewer patches, shorter patch
boundaries, and fewer small patches and narrow regions.
Piecewise developable approximation, evolutionary genetic algorithm, conformal mapping, cone singularity
Generating such a piecewise developable mesh is
challenging due to these combinatorial constraints and mutually restrictive objectives.
To adapt to these objectives and constraints, we first customize the evolutionary genetic
algorithm to construct the partition and then deform each patch to be discrete developable
to obtain a piecewise developable mesh.
In our genetic algorithm, a chromosome is a partition of the input.
The main challenge for tailor-making the genetic algorithm is to compute the approximation error for evaluating
the chromosome's fitness function, including the desired objectives and constraints. To resolve this challenge,
we innovatively use the techniques of conformal mappings.
Figure 2: The generation of one chromosome. (a) The input. (b) The set of cone singularities. (c) The minimum spanning tree connecting all cone singularities. (d)
The initial partition whose boundary contains this minimum spanning tree.
Then it performs genetic operations to evolve the population for finding a chromosome with a small fitness value
until the termination conditions are satisfied.
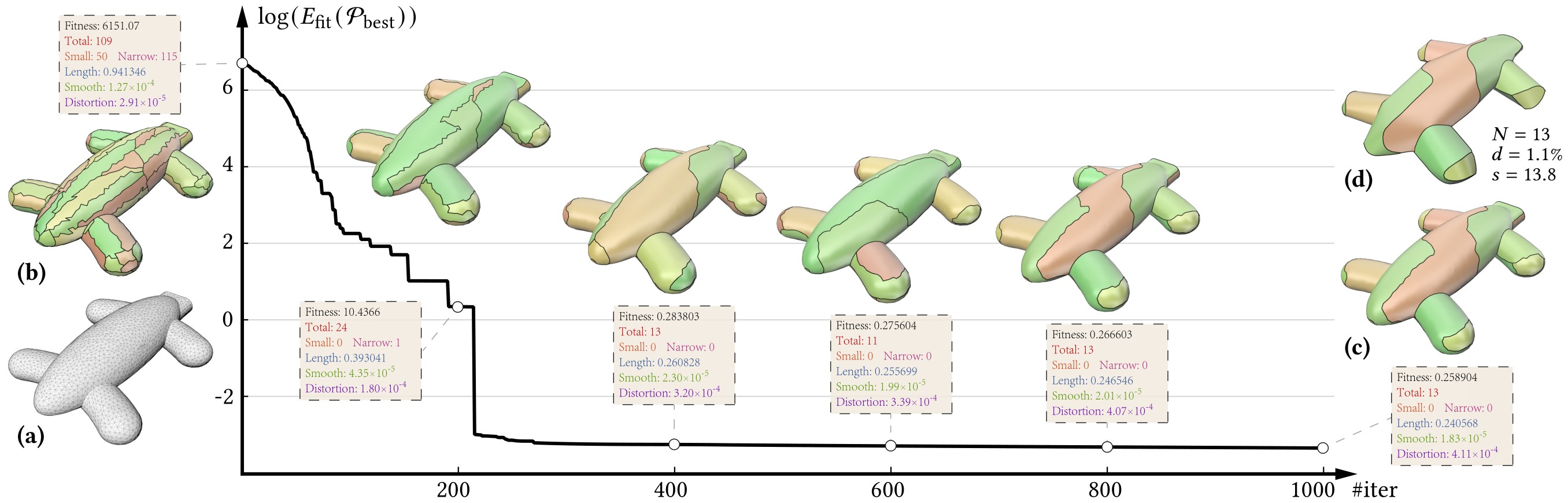
Figure 3: Workflow of our method. Given an input mesh M (a), our algorithm first generates an initial population A
(the best chromosome in the initial population is shown in (b)), then evolves the population for finding a chromosome with
a small fitness value (c), and finally deform patches to be piecewise developable to generate the result (d).
The graph plots the fitness of the best chromosome P best in the population as a function of the number of evolutionary iterations.
The red, orange, pink, blue, green, and purple numbers denote Etotal(Pbest), Esmall(Pbest),
Enarrow(Pbest), Elength(Pbest), Esmooth(Pbest),
and ε(Pbest), respectively. The sudden drop of the fitness function near the 200th iteration
is due to the disappearance of the narrow regions.
Specifically, the operations include selection, crossover, and mutation.
Given the best partition, we deform the input mesh to be piecewise developable while possessing a small approximation error.
The genetic algorithm starts from an initial population consisting of many chromosomes (i.e., partitions).

Code (15.3M)
Supplement and Data
Demo (*.mp4) (78.6M)
We would like to thank the anonymous reviewers for their constructive suggestions and comments.
This work is partially supported by the National Key R&D Program of China (2022YFB3303400), the
National Natural Science Foundation of China (62272429, 62025207) and the Major Project of Science
and Technology of Anhui Province (202203a05020050).
@article {zhao2023evolutionary,
title = {Evolutionary Piecewise Developable Approximations},
author = {Zhao, Zheng-Yu and Li, Mo and Zhang, Zheng and Fang, Qing and Liu, Ligang and Fu, Xiao-Ming}
journal = {ACM Transactions on Graphics},
volume={42},
number={4},
pages={1--13},
year = {2023}
}