
Teaser: High-order shell and application. Given a low-quality triangular mesh (a), we construct a high-order shell (b). Then, we remesh the low-quality mesh within the high-order shell to generate a new mesh, which is further tetrahedrized (c). We deform the mesh in (c) to generate a deformed mesh (d) using the settings in (a). Finally, the displacement field of the deformation is bijectively transferred back to the input to produce a deformation of the input mesh (e).
Abstract
We propose a new structure called a higher-order shell, which is composed of a set of triangular prisms.
Each triangular prism is enveloped by three Bezier triangles (top, middle, and bottom) and three side surfaces, each of which is trimmed from a bilinear surface.
Moreover, we define a continuous vector field to smoothly and bijectively transfer attributes between two surfaces inside the shell.
Since the higher-order shell has several hard construction constraints, we apply an interior-point strategy to robustly and automatically construct a high-order shell for an input mesh.
Specifically, the strategy starts from a valid linear shell with a small thickness. Then, the shell is optimized until the specified thickness is reached, where explicit checks ensure that the constraints are always satisfied.
We extensively test our method on more than 8300 models, demonstrating its robustness and performance.
Compared to state-of-the-art methods, our bijective projection is smoother, and the space between the shell and input mesh is more uniform.
high-order shell, attribute transfer, smooth projection, bijective
The generation of the described prisms presents two challenges.
First, it is difficult to precisely make the edges of the three Bezier triangles lie on the bilinear surfaces.
Second, assuming that we can find a way to solve the first challenge, we still need to ensure that the projection along the vector field has a chance to become a bijective map between two surfaces inside the shell.
Then, proposing a sufficient condition to judge whether such a projection can become a bijection becomes challenging.
To overcome the first challenge, we establish a \emph{placement condition} to constrain the placement of control points of the three Bezier triangles, enabling the Bezier triangles' edges to lie on
the bilinear surfaces accurately and the Bezier triangles to approximate the input surface.
After constructing the Bezier triangles accordingly, the vector field can be regarded as the image of the isoparametric lines of a complex domain
under the isoparametric transformation. Then, if the isoparametric transformation is bijective in the complex domain, the projection along the vector field can be a bijection.
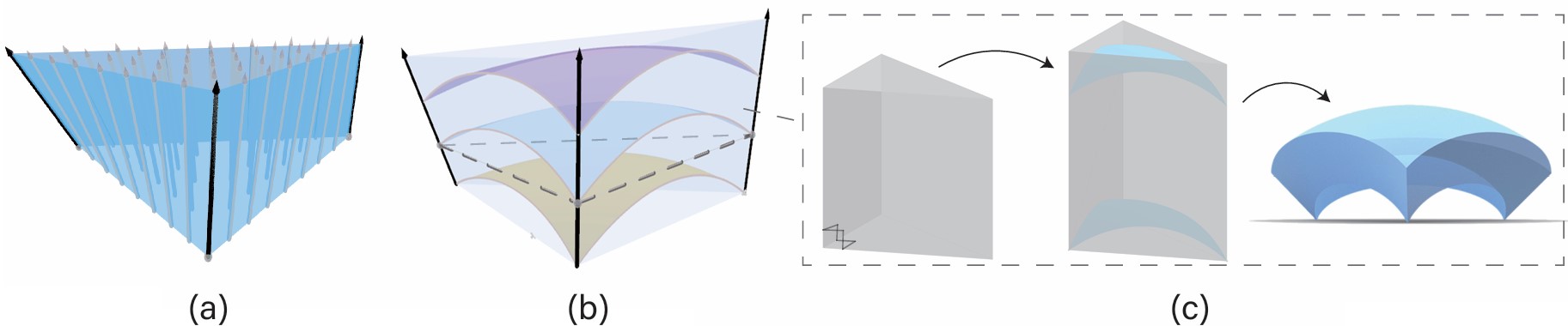
Figure 2: The definition of high-order shell. (a) The continuous vector field. (b) The triangular prism envelopes by three
Bezier triangles and three side bilinear surfaces. (c) The generation of the bezier triangles such that the boundaries of thr Bezier
triangle conform to the bilinear patch.
To efficiently construct sparse and high-quality high-order shells, we start with a linear shell of minimal initial thickness
and continuously perform local operations to optimize the shell structure until the target thickness is reached. During the
optimization process, we use an interior-point method strategy. After each local operation, we perform conditional fitting
of the Bezier triangles and reject any local operations that would cause the shell space to lose its bijective properties.
Figure 3: Workflow of our method. Given an input mesh, our algorithm is initialized with a dense linear shell, where the vector field is defined to align with the image of the
side bilinear surfaces' parametric lines in one direction. Then, we iteratively perform local remeshing operations to optimize and
simplify the shell until the specified thickness is reached. In each operation, we place the control points based on the placement
condition and check whether any constraint is violated. If there is a violation, we reject the operation.
Specifically, the operations include collapse, flip, zoom and optimize.
We terminate the algorithm when no local operations can be further conducted.
In this paper, we define a new high-order triangular prism shell space and propose a progressive robust construction algorithm. High-order triangular prisms consist of three Bezier triangles and three bilinear surfaces.
To achieve a smooth mapping, we use linear interpolation of three vectors to obtain a vector field within the prism.
By exploring conditions that make the boundaries of the Bezier triangles conform to the vector field boundaries and are easy
to fit, we obtain high-order triangular prisms composed of three Bezier triangles and three bilinear surfaces.
We would like to thank the anonymous reviewers for their constructive suggestions and comments.
This work is partially supported by the National Natural Science Foundation of China (62272429, 62025207).
@article {liu2024curveshell,
title = {Smooth Bijective Projection in a High-order Shell},
author = {Liu, Shibo and Ji, Yang and Guo, Jia-Peng and Liu, Ligang and Fu, Xiao-Ming}
journal = {ACM Transactions on Graphics},
volume={43},
number={4},
pages={1--13},
year = {2024}
}